
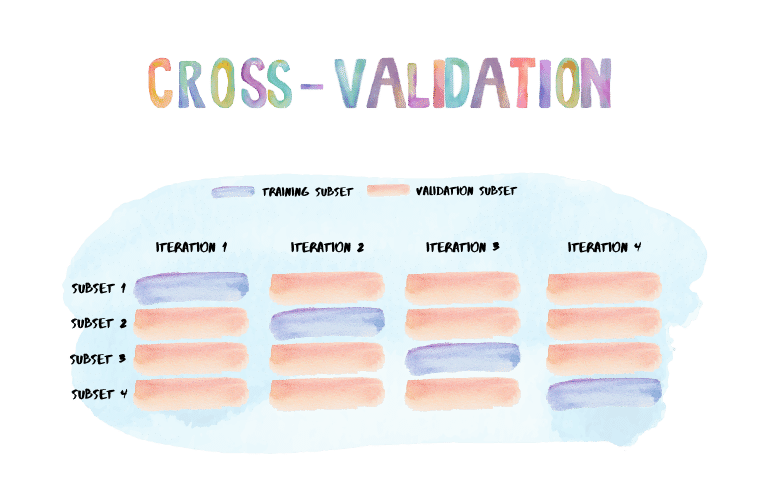
Section 14 Cross-Validation
14.1 Test and Training Error Rate
In previous section, we discuss the distinction between the test error rate and the training error rate as follows:
The test error is the average error that results from using a statistical learning method to predict the response on a new observation— that is, a measurement that was not used in training the method. The test error can be easily calculated if a designated test set is available. Unfortunately, this is usually not the case.
The training error can be easily calculated by applying the statistical learning method to the observations used in its training. However, the training error rate often is quite different from the test error rate, and in particular the former can dramatically underestimate the latter.
In this section, we instead consider a class of methods that estimate the test error rate by holding out a subset of the training observations from the fitting process, and then applying the statistical learning method to those held out observations.
14.2 The Validation Set Approach
The validation set approach is a cross-validation technique in Machine learning. In the Validation Set approach, the dataset which will be used to build the model is divided randomly into 2 parts namely training set and validation set(or testing set).
Steps Involved in the Validation Set Approach:
A random splitting of the dataset into a certain ratio(generally 70-30 or 80-20 ratio is preferred)
Training of the model on the training data set
The resultant model is applied to the validation set
Model’s accuracy is calculated through prediction error by using model performance metrics
The validation set approach is illustrated in Figure 14.1. A set of \(n\) observations are randomly split into a training set (shown in blue, containing observations 7, 22, and 13, among others) and a validation set (shown in beige, and containing observation 91, among others). The statistical learning method is fit on the training set, and its performance is evaluated on the validation set.
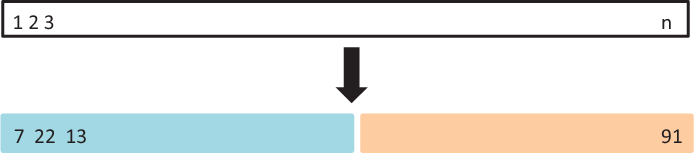
Figure 14.1: A schematic display of CV
The validation set approach is conceptually simple and is easy to implement. But it has two potential drawbacks:
the validation estimate of the test error rate can be highly variable, depending on precisely which observations are included in the training set and which observations are included in the validation set.
In the validation approach, only a subset of the observations—those that are included in the training set rather than in the validation set—are used to fit the model. Since statistical methods tend to perform worse when trained on fewer observations, this suggests that the validation set error rate may tend to overestimate the test error rate for the model fit on the entire data set.
14.3 Leave-One-Out Cross-Validation
Leave-one-out cross-validation (LOOCV) is closely related to the validation leave-oneout crossvalidation set approach of Section Validation Set Approach, but it attempts to address that method’s drawbacks.
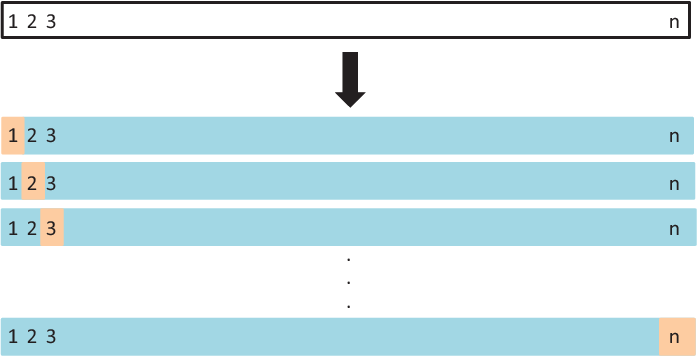
Figure 14.2: A schematic display of LOOCV
A display of LOOCV is illustrated in Figure 14.2. A set of \(n\) data points is repeatedly split into a training set (shown in blue) containing all but one observation (\(n-1\)), and a validation set that contains only that observation (shown in beige). The test error is then estimated by averaging the \(n\) resulting \(MSE\)’s. The first training set contains all but observation 1, the second training set contains all but observation 2, and so forth.
The benefit of so many fit and evaluated models is a more robust estimate of model performance as each row of data is given an opportunity to represent the entirety of the test dataset. Specifically, LOOCV has a couple of major advantages over the validation set approach:
- First, it has far less bias. In LOOCV, we repeatedly fit the statistical learning method using training sets that contain \(n − 1\) observations, almost as many as are in the entire data set. This is in contrast to the validation set approach, in which the training set is typically around half the size of the original data set. Consequently, the LOOCV approach tends not to overestimate the test error rate as much as the validation set approach does.
Second, there is no randomness in the training/validation set splits. In contrast to the validation approach which will yield different results when applied repeatedly due to randomness in the training/validation set splits, performing LOOCV multiple times will always yield the same results.
However, this method has the maximum computational cost. It requires one model to be created and evaluated for each example in the training dataset and thus, is not suggested to apply when there is very lage number of \(n\).
Don’t Use LOOCV: Large datasets or costly models to fit.
Use LOOCV: Small datasets or when estimated model performance is critical.
14.4 \(k\)-Fold Cross-Validation
An alternative to LOOCV is k-fold CV. This approach involves randomly k-fold CV dividing the set of observations into \(k\) groups, or folds, of approximately equal size. The first fold is treated as a validation set, and the method is fit on the remaining \(k − 1\) folds.
It is not hard to see that LOOCV is a special case of k-fold CV in which \(k\) is set to equal \(n\). In practice, one typically performs k-fold CV using \(k = 5\) or \(k = 10\).
The most obvious advantage is computational. LOOCV requires fitting the statistical learning method \(n\) times. This has the potential to be computationally expensive. Some statistical learning methods have computationally intensive fitting procedures, and so performing LOOCV may pose computational problems. In contrast, performing 10-fold CV requires fitting the learning procedure only ten times, which may be much more feasible.
But putting computational issues aside, a less obvious but potentially more important advantage of k-fold CV is that it often gives more accurate estimates of the test error rate than does LOOCV. This has to do with a bias-variance trade-off.
14.5 Bias-Variance Trade-Off for k-Fold Cross-Validation
It was mentioned in Section Validation Set Approach that the validation set approach can lead to overestimates of the test error rate, since in this approach the training set used to fit the statistical learning method contains only half the observations of the entire data set.
Using this logic, it is not hard to see that LOOCV will give approximately unbiased estimates of the test error, since each training set contains \(n−1\) observations, which is almost as many as the number of observations in the full data set.
And performing k-fold CV for, say, \(k = 5\) or \(k = 10\) will lead to an intermediate level of bias - fewer than in the LOOCV approach, but substantially more than in the validation set approach. Therefore, from the perspective of bias reduction, it is clear that LOOCV is to be preferred to k-fold CV.
To summarize, there is a bias-variance trade-off associated with the choice of k in k-fold cross-validation. Typically, given these considerations, one performs k-fold cross-validation using \(k = 5\) or \(k = 10\), as these values have been shown empirically to yield test error rate estimates that suffer neither from excessively high bias nor from very high variance.